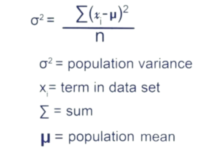Jika Anda tertarik dalam dunia matematika dan statistik, pasti tidak asing lagi dengan Rumus Std. Dalam artikel blog ini, kami akan memberikan panduan lengkap dan komprehensif tentang Rumus Std, mulai dari pengertian dasar hingga penggunaan dalam berbagai bidang.
Rumus Std, juga dikenal sebagai Rumus Standar, adalah rumus yang digunakan untuk mengukur sejauh mana data tersebar dalam satu set data. Dengan menggunakan Rumus Std, kita dapat menghitung deviasi standar, yang merupakan ukuran statistik yang penting dalam analisis data.
Pengertian Rumus Std
Pada bagian ini, kami akan menjelaskan secara detail pengertian Rumus Std. Rumus Std merupakan alat yang digunakan untuk mengukur sejauh mana data tersebar dalam satu set data. Dalam matematika dan statistik, deviasi standar digunakan untuk menunjukkan sejauh mana nilai-nilai dalam kumpulan data mendekati atau menjauhi rata-ratanya.
Deviasi standar adalah akar kuadrat dari variansi. Variansi adalah rata-rata dari kuadrat perbedaan antara setiap nilai dalam kumpulan data dengan rata-ratanya. Dengan menggunakan rumus deviasi standar, kita dapat menghitung dan memahami sebaran data dengan lebih jelas.
Formula dan Cara Menghitung Deviasi Standar
Untuk menghitung deviasi standar, kita perlu mengikuti beberapa langkah matematika. Pertama, kita perlu menghitung rata-rata dari kumpulan data tersebut. Kemudian, kita menghitung perbedaan antara setiap nilai dalam kumpulan data dengan rata-ratanya.
Setelah itu, kita memangkatkan setiap selisih tersebut, menjumlahkannya, kemudian membaginya dengan jumlah data dikurangi satu. Akhirnya, kita mengambil akar kuadrat dari hasil tersebut untuk mendapatkan deviasi standar.
Contoh Perhitungan Deviasi Standar
Misalnya, kita memiliki kumpulan data berikut: 10, 12, 14, 16, 18. Pertama, kita hitung rata-ratanya dengan menjumlahkan semua nilai dalam kumpulan data dan membaginya dengan jumlah data, yaitu 5. Rata-rata dari data ini adalah 14.
Selanjutnya, kita hitung selisih antara setiap nilai dan rata-rata. Untuk nilai 10, selisihnya adalah -4. Untuk nilai 12, selisihnya adalah -2. Untuk nilai 14, selisihnya adalah 0. Untuk nilai 16, selisihnya adalah 2. Dan untuk nilai 18, selisihnya adalah 4.
Kemudian, kita memangkatkan setiap selisih tersebut. Untuk nilai 10, hasil pangkatnya adalah 16. Untuk nilai 12, hasil pangkatnya adalah 4. Untuk nilai 14, hasil pangkatnya adalah 0. Untuk nilai 16, hasil pangkatnya adalah 4. Dan untuk nilai 18, hasil pangkatnya adalah 16.
Setelah itu, kita menjumlahkan semua hasil pangkat tersebut, yaitu 40. Kemudian, kita bagi hasil tersebut dengan jumlah data dikurangi satu, yaitu 5-1=4. Hasil bagi adalah 10.
Akhirnya, kita mengambil akar kuadrat dari hasil tersebut. Akar kuadrat dari 10 adalah sekitar 3.16. Jadi, deviasi standar dari kumpulan data ini adalah 3.16.
Penggunaan Rumus Std dalam Analisis Data
Rumus Std memiliki penggunaan yang luas dalam analisis data. Dalam bagian ini, kami akan menjelaskan bagaimana Rumus Std dapat digunakan untuk mengukur variabilitas data, mengidentifikasi outlier, dan membandingkan distribusi data.
Pengukuran Variabilitas Data
Deviasi standar digunakan untuk mengukur variabilitas data dalam satu set data. Semakin besar deviasi standar, semakin besar sebaran data tersebut. Dengan mengukur deviasi standar, kita dapat mengetahui sejauh mana nilai-nilai dalam kumpulan data tersebar dan apakah data tersebut homogen atau heterogen.
Identifikasi Outlier
Outlier adalah nilai yang secara signifikan berbeda dari nilai-nilai lain dalam kumpulan data. Dengan menggunakan deviasi standar, kita dapat mengidentifikasi outlier dengan membandingkan nilai-nilai individual dengan rata-rata dan deviasi standar kumpulan data tersebut.
Jika nilai individual berada di luar rentang rata-rata plus atau minus beberapa kali deviasi standar, maka kita dapat menganggapnya sebagai outlier. Identifikasi outlier ini penting dalam analisis data karena outlier dapat mempengaruhi hasil analisis secara keseluruhan.
Perbandingan Distribusi Data
Dalam analisis data, seringkali kita perlu membandingkan distribusi data dari dua atau lebih kelompok atau kondisi yang berbeda. Deviasi standar dapat digunakan untuk membandingkan sebaran data antara kelompok-kelompok tersebut.
Jika deviasi standar suatu kelompok lebih besar daripada kelompok lainnya, maka kita dapat menyimpulkan bahwa sebaran data dalam kelompok tersebut lebih besar atau lebih variabel. Hal ini dapat memberikan informasi yang berharga dalam memahami perbedaan antar kelompok atau kondisi dalam analisis data.
Kelebihan dan Kekurangan Penggunaan Rumus Std
Tidak ada metode yang sempurna, begitu juga dengan Rumus Std. Pada bagian ini, kami akan membahas kelebihan dan kekurangan penggunaan Rumus Std dalam analisis data.
Kelebihan Penggunaan Rumus Std
Salah satu kelebihan penggunaan Rumus Std adalah kemampuannya dalam mengukur sebaran data yang lebih kompleks. Deviasi standar dapat mengakomodasi perbedaan dalam data yang mungkin terdapat pola-pola yang lebih rumit dan tidak terduga.
Deviasi standar juga memberikan ukuran yang lebih intuitif dalam memahami sebaran data daripada variansi. Karena deviasi standar dihitung dalam satuan yang sama dengan data aslinya, kita dapat dengan mudah membandingkan nilai deviasi standar antara kelompok data yang berbeda atau dalam skala yang sama.
Kekurangan Penggunaan Rumus Std
Salah satu kekurangan penggunaan Rumus Std adalah ketidakpekaannya terhadap bentuk distribusi data. Deviasi standar tidak memberikan informasi tentang bentuk distribusi data tersebut, hanya mengukur sebaran data dalam bentuk nilai absolut.
Deviasi standar juga rentan terhadap pengaruh outlier. Jika terdapat outlier dalam kumpulan data, deviasi standar dapat menjadi tidak representatif terhadap sebaran data yang sebenarnya.
Perbedaan antara Rumus Std dan Rumus Variansi
Seringkali, Rumus Std dan Rumus Variansi dapat membingungkan. Di sini, kami akan menjelaskan perbedaan mendasar antara keduanya.
Perbedaan dalam Formula
Perbedaan utama antara Rumus Std dan Rumus Variansi terletak pada formula yang digunakan. Rumus Variansi menghitung rata-rata dari kuadrat perbedaan antara setiap nilai dalam kumpulan data dengan rata-ratanya, sedangkan Rumus Std mengambil akar kuadrat dari variansi tersebut.
Perbedaan dalam Ukuran
Perbedaan penting lainnya adalah ukuran yang dihasilkan oleh kedua rumus tersebut. Rumus Variansi menghasilkan ukuran yang berbeda dari kumpulan data aslinya, yaitu variansi. Sedangkan Rumus Std menghasilkan ukuran yang memiliki satuan yang sama dengan data aslinya, yaitu deviasi standar.
Contoh Penerapan Rumus Std dalam Bidang Statistik
Statistik adalah salah satu bidang yang sangat bergantung pada Rumus Std. Dalam bagian ini, kami akan memberikan contoh nyata pener
Contoh Penerapan Rumus Std dalam Bidang Statistik
Statistik adalah salah satu bidang yang sangat bergantung pada Rumus Std. Dalam bagian ini, kami akan memberikan contoh nyata penerapan Rumus Std dalam bidang statistik.
Uji Hipotesis
Rumus Std sering digunakan dalam uji hipotesis untuk menentukan apakah suatu perbedaan antara dua kelompok data adalah signifikan secara statistik. Dalam uji hipotesis, kita membandingkan rata-rata dari dua kelompok data dan menggunakan deviasi standar untuk mengukur sebaran data dan variabilitas antar kelompok.
Contohnya, dalam uji hipotesis untuk membandingkan rata-rata tinggi badan antara pria dan wanita, kita akan menggunakan Rumus Std untuk menghitung deviasi standar dalam masing-masing kelompok. Deviasi standar yang lebih besar menunjukkan bahwa tinggi badan dalam kelompok tersebut lebih bervariasi.
Analisis Regresi
Rumus Std juga digunakan dalam analisis regresi, yang merupakan metode statistik untuk mempelajari hubungan antara variabel dependen dan variabel independen. Dalam analisis regresi, deviasi standar digunakan untuk mengukur seberapa akurat model regresi dalam memprediksi nilai-nilai dependen.
Misalnya, dalam analisis regresi untuk memprediksi harga rumah berdasarkan luas tanah, jumlah kamar tidur, dan lokasi, kita menggunakan Rumus Std untuk mengukur sebaran data harga rumah yang sebenarnya. Semakin kecil deviasi standar, semakin akurat model regresi dalam memprediksi harga rumah.
Pengambilan Keputusan Berdasarkan Data Statistik
Rumus Std juga digunakan dalam pengambilan keputusan berdasarkan data statistik. Dalam situasi di mana ada risiko atau ketidakpastian, deviasi standar dapat memberikan informasi penting untuk memahami sebaran data dan mengukur risiko yang terkait.
Misalnya, dalam pengambilan keputusan investasi, deviasi standar digunakan untuk mengukur volatilitas harga saham atau aset lainnya. Semakin tinggi deviasi standar, semakin besar fluktuasi harga, yang menunjukkan risiko yang lebih tinggi. Informasi ini dapat membantu investor dalam membuat keputusan yang cerdas dan mengelola risiko investasi mereka.
Penerapan Rumus Std dalam Bidang Keuangan
Rumus Std juga memiliki penggunaan yang luas dalam bidang keuangan. Dalam bagian ini, kami akan menjelaskan bagaimana Rumus Std dapat digunakan untuk mengukur risiko investasi, mengevaluasi kinerja portofolio, dan mengidentifikasi volatilitas harga.
Mengukur Risiko Investasi
Rumus Std digunakan dalam mengukur risiko investasi, terutama dalam pasar saham. Deviasi standar adalah salah satu ukuran risiko yang paling umum digunakan oleh investor dan analis keuangan.
Deviasi standar yang tinggi menunjukkan volatilitas harga yang lebih besar, yang berarti investasi tersebut memiliki risiko yang lebih tinggi. Dalam pengambilan keputusan investasi, investor sering memperhatikan deviasi standar untuk memahami seberapa besar fluktuasi harga yang mungkin terjadi.
Mengevaluasi Kinerja Portofolio
Rumus Std juga digunakan untuk mengevaluasi kinerja portofolio investasi. Deviasi standar digunakan sebagai ukuran volatilitas total portofolio, yang menggabungkan volatilitas masing-masing aset dalam portofolio.
Dengan memperhatikan deviasi standar, investor dapat membandingkan risiko dan potensi pengembalian dari berbagai portofolio investasi. Portofolio dengan deviasi standar yang lebih rendah cenderung lebih stabil dan kurang bergejolak dibandingkan dengan portofolio dengan deviasi standar yang lebih tinggi.
Identifikasi Volatilitas Harga
Rumus Std juga digunakan untuk mengidentifikasi volatilitas harga dalam pasar keuangan. Deviasi standar dapat memberikan informasi tentang seberapa besar fluktuasi harga yang mungkin terjadi dalam satu aset atau pasar tertentu.
Analisis volatilitas harga sangat penting dalam perdagangan saham, pasar valuta asing, dan instrumen keuangan lainnya. Dengan memahami volatilitas harga, investor dan pedagang dapat mengambil keputusan yang lebih baik dalam manajemen risiko, alokasi aset, dan pengambilan posisi dalam pasar keuangan.
Penerapan Rumus Std dalam Bidang Ilmu Sosial
Rumus Std juga memiliki penerapan yang penting dalam bidang ilmu sosial. Dalam bagian ini, kami akan menjelaskan bagaimana Rumus Std dapat digunakan dalam survei, penelitian sosial, dan analisis data kualitatif.
Survei dan Penelitian Sosial
Rumus Std digunakan dalam analisis data survei dan penelitian sosial untuk mengukur variabilitas dan sebaran data. Dalam survei, deviasi standar dapat digunakan untuk melihat seberapa heterogen tanggapan responden terhadap pertanyaan-pertanyaan survei.
Deviasi standar yang tinggi menunjukkan variasi pendapat yang lebih besar, sedangkan deviasi standar yang rendah menunjukkan konsistensi pendapat. Informasi ini penting dalam penelitian sosial untuk mengidentifikasi perbedaan, kecenderungan, dan pola dalam tanggapan responden.
Analisis Data Kualitatif
Rumus Std juga dapat digunakan dalam analisis data kualitatif, meskipun dalam konteks ini penggunaannya sedikit berbeda. Dalam analisis data kualitatif, deviasi standar dapat digunakan untuk mengukur variasi dan sebaran dalam interpretasi atau penafsiran data yang dilakukan oleh peneliti.
Deviasi standar yang tinggi menunjukkan variasi dalam interpretasi atau penafsiran data, sementara deviasi standar yang rendah menunjukkan konsistensi dalam interpretasi atau penafsiran data. Informasi ini dapat membantu peneliti dalam memahami sejauh mana kesepakatan atau perbedaan dalam interpretasi dan penafsiran data kualitatif.
Tips dan Trik untuk Menggunakan Rumus Std dengan Efektif
Menggunakan Rumus Std dengan efektif membutuhkan pemahaman yang baik tentang konsep dan teknik penghitungannya. Dalam bagian ini, kami akan memberikan tips dan trik untuk menggunakan Rumus Std dengan efektif dalam analisis data.
Pahami Konsep Dasar
Sebelum menggunakan Rumus Std, penting untuk memahami konsep dasar di baliknya. Pahami pengukuran sebaran data, deviasi standar, dan hubungannya dengan rata-rata dan variansi. Dengan pemahaman yang kuat tentang konsep ini, Anda akan dapat menginterpretasikan hasil dengan lebih baik.
Pastikan Data Anda Tepat
Pastikan data yang Anda gunakan untuk menghitung deviasi standar akurat dan relevan dengan pertanyaan atau tujuan analisis Anda. Periksa kembali data Anda untuk menghindari kesalahan penginputan atau pengumpulan data yang dapat mempengaruhi hasil akhir.
Gunakan Alat Bantu Komputasi
Untuk menghitung deviasi standar dengan cepat dan akurat, gunakan alat bantu komputasi seperti spreadsheet atau perangkat lunak statistik. Alat ini akan membantu Anda menghemat waktu dan mengurangi kesalahan perhitungan manusia.
Interpretasikan Hasil dengan Konteks
Saat menginterpretasikan hasil deviasi standar, pastikan Anda melakukannya dengan konteks yang tepat. Pertimbangkan tujuan analisis Anda, karakteristik data, dan pertanyaan penelitian yang ingin Anda jawab. Hindari kesalahan interpretasi dengan mempertimbangkan konteks secara menyeluruh.
Perbandingkan dengan Nilai Tertentu
Untuk memperoleh pem
Tips dan Trik untuk Menggunakan Rumus Std dengan Efektif
Menggunakan Rumus Std dengan efektif membutuhkan pemahaman yang baik tentang konsep dan teknik penghitungannya. Dalam bagian ini, kami akan memberikan tips dan trik untuk menggunakan Rumus Std dengan efektif dalam analisis data.
Pahami Konsep Dasar
Sebelum menggunakan Rumus Std, penting untuk memahami konsep dasar di baliknya. Pahami pengukuran sebaran data, deviasi standar, dan hubungannya dengan rata-rata dan variansi. Dengan pemahaman yang kuat tentang konsep ini, Anda akan dapat menginterpretasikan hasil dengan lebih baik.
Pastikan Data Anda Tepat
Pastikan data yang Anda gunakan untuk menghitung deviasi standar akurat dan relevan dengan pertanyaan atau tujuan analisis Anda. Periksa kembali data Anda untuk memastikan tidak ada kesalahan penginputan atau pengumpulan data yang dapat mempengaruhi hasil akhir. Jika memungkinkan, gunakan teknik pengambilan sampel yang representatif untuk mendapatkan hasil yang lebih akurat.
Gunakan Alat Bantu Komputasi
Untuk menghitung deviasi standar dengan cepat dan akurat, manfaatkan alat bantu komputasi seperti spreadsheet atau perangkat lunak statistik. Alat ini akan membantu Anda menghemat waktu dan mengurangi kesalahan perhitungan manusia. Selain itu, alat bantu komputasi juga dapat memberikan visualisasi data yang memudahkan pemahaman dan analisis.
Perhatikan Skala Data
Ketika menggunakan Rumus Std, perhatikan skala data yang Anda gunakan. Jika data Anda memiliki skala yang sangat berbeda, seperti memiliki satuan yang berbeda, maka hasil deviasi standar juga akan bervariasi. Pastikan untuk menormalisasi atau menstandarisasi data jika perlu, agar perbandingan antar kelompok data atau variabel lebih tepat.
Perbandingkan dengan Nilai Tertentu
Untuk memperoleh pemahaman yang lebih baik tentang sebaran data, perbandingkan deviasi standar dengan nilai tertentu yang relevan. Misalnya, bandingkan deviasi standar dengan rata-rata atau nilai referensi lainnya untuk melihat sejauh mana data tersebar. Hal ini akan membantu Anda dalam menginterpretasikan nilai deviasi standar dengan lebih kontekstual.
Pahami Batasan dan Kelemahan Rumus Std
Setiap metode atau rumus memiliki batasan dan kelemahan. Pahami batasan dan kelemahan Rumus Std sehingga Anda dapat menggunakan hasilnya dengan bijak. Misalnya, deviasi standar tidak dapat mengidentifikasi pola dalam distribusi data, dan rentan terhadap pengaruh outlier. Oleh karena itu, penting untuk melihat secara menyeluruh karakteristik data dan mempertimbangkan metode lain jika diperlukan.
Sumber Daya dan Referensi untuk Memperdalam Pemahaman Anda
Untuk memperdalam pemahaman Anda tentang Rumus Std dan aplikasinya, berikut adalah beberapa sumber daya dan referensi yang dapat Anda manfaatkan:
Buku tentang Statistik dan Analisis Data
Ada banyak buku yang membahas secara rinci tentang statistik dan analisis data, termasuk Rumus Std. Beberapa buku yang sangat direkomendasikan adalah “Statistik Dasar untuk Penelitian Sosial” karya Allan G. Bluman, “Statistik Terapan untuk Bisnis dan Ekonomi” karya David P. Doane dan Lori E. Seward, dan “Statistik Terapan untuk Ilmu-ilmu Sosial” karya Rachel A. Gordon.
Jurnal dan Artikel Ilmiah
Berlangganan jurnal dan membaca artikel ilmiah dapat membantu Anda memperoleh wawasan terbaru dalam bidang statistik dan aplikasi Rumus Std. Jurnal seperti Journal of Statistical Software, Journal of Applied Statistics, dan Journal of Data Science menyediakan publikasi berkualitas tinggi dalam bidang ini.
Kursus Online dan Tutorial
Ada banyak kursus online dan tutorial yang tersedia untuk mempelajari statistik dan aplikasi Rumus Std secara interaktif. Platform seperti Coursera, Udemy, dan Khan Academy menawarkan kursus-kursus yang dikembangkan oleh para ahli, dengan materi yang lengkap dan latihan praktis untuk memperdalam pemahaman Anda.
Komunitas dan Forum Diskusi
Bergabung dengan komunitas statistik atau forum diskusi online dapat memberikan kesempatan untuk berinteraksi dengan para ahli dan diskusi tentang Rumus Std. Anda dapat berbagi pengalaman, bertanya pertanyaan, dan memperoleh wawasan dari orang-orang dengan latar belakang dan pengetahuan yang beragam.
Sumber Online dan Website Resmi
Ada banyak sumber online dan website resmi yang menyediakan informasi dan panduan tentang Rumus Std. Beberapa sumber yang dapat Anda manfaatkan adalah Khan Academy, Stat Trek, dan website resmi lembaga statistik seperti BPS (Badan Pusat Statistik) atau BPS (Bureau of Labor Statistics).
Dengan memanfaatkan sumber daya ini, Anda dapat memperdalam pemahaman tentang Rumus Std dan meningkatkan keterampilan analisis data Anda. Teruslah belajar, praktikkan, dan eksplorasi berbagai sumber daya yang tersedia untuk menjadi ahli dalam penggunaan Rumus Std.