Selamat datang di blog kami! Pada artikel ini, kami akan membahas secara rinci tentang rumus standar deviasi di Excel dan bagaimana Anda dapat menggunakannya. Standar deviasi adalah ukuran yang berguna untuk mengukur sejauh mana data tersebar dari nilai rata-ratanya. Dalam analisis statistik, rumus standar deviasi sangat penting untuk menghitung variabilitas dalam data Anda.
Sebelum kita membahas rumusnya, mari kita tinjau terlebih dahulu apa itu standar deviasi. Standar deviasi adalah akar kuadrat dari varians. Varians, di sisi lain, adalah rata-rata kuadrat perbedaan antara setiap titik data dan rata-rata data. Dengan menggunakan rumus standar deviasi, Anda dapat menentukan seberapa jauh titik data individu tersebar dari rata-rata, sehingga memberikan gambaran yang lebih lengkap tentang distribusi data Anda.
Pengenalan Standar Deviasi
Pengenalan Standar Deviasi
Standar deviasi adalah ukuran statistik yang digunakan untuk mengukur sejauh mana data tersebar dari nilai rata-ratanya. Dalam analisis statistik, rumus standar deviasi sangat penting karena memberikan informasi tentang variasi atau dispersi data Anda. Semakin tinggi standar deviasi, semakin besar variasi dalam data.
Kenapa Standar Deviasi Penting?
Standar deviasi penting karena memberikan gambaran yang lebih lengkap tentang distribusi data Anda dibandingkan hanya dengan menggunakan nilai rata-rata. Dengan mengetahui standar deviasi, Anda dapat menentukan seberapa jauh titik data individu tersebar dari rata-rata. Hal ini membantu Anda dalam mengidentifikasi apakah data Anda homogen atau heterogen.
Bagaimana Standar Deviasi Dipergunakan dalam Analisis Data?
Dalam analisis data, standar deviasi digunakan untuk membandingkan variasi antara kelompok data yang berbeda atau untuk melihat sejauh mana observasi individual dari kelompok data tertentu. Standar deviasi juga dapat digunakan untuk menguji signifikansi perbedaan antara kelompok data.
Rumus Standar Deviasi di Excel
Rumus Standar Deviasi di Excel
Excel menyediakan beberapa fungsi untuk menghitung standar deviasi, tergantung pada jenis data yang Anda miliki. Fungsi yang paling umum digunakan adalah STDEV.P dan STDEV.S. STDEV.P digunakan untuk menghitung standar deviasi pada populasi, sementara STDEV.S digunakan untuk menghitung standar deviasi pada sampel. Rumus standar deviasi di Excel menggunakan fungsi-fungsi ini dan dapat diterapkan dengan mudah pada rentang data tertentu.
Penggunaan Rumus Standar Deviasi di Excel
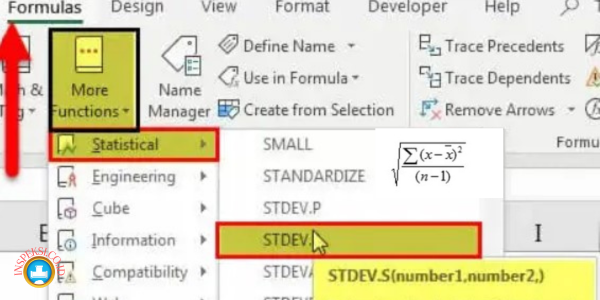
Langkah-langkah untuk menggunakan rumus standar deviasi di Excel cukup sederhana. Pertama, Anda perlu memilih sel atau rentang sel yang berisi data yang ingin Anda hitung standar deviasinya. Kemudian, Anda dapat menggunakan fungsi STDEV.P atau STDEV.S, diikuti oleh rentang data yang telah Anda pilih. Setelah Anda menekan Enter, Excel akan menghitung standar deviasi dan menampilkan hasilnya di sel yang Anda pilih.
Contoh Penggunaan Rumus Standar Deviasi di Excel
Contoh Penggunaan Rumus Standar Deviasi di Excel
Untuk memberikan pemahaman yang lebih baik tentang bagaimana rumus standar deviasi di Excel digunakan, berikut adalah contoh penggunaannya dalam situasi nyata:
Contoh 1: Anda memiliki data ketinggian (dalam sentimeter) dari 100 individu. Anda ingin menghitung standar deviasi dari data ini untuk mengetahui seberapa bervariasinya ketinggian individu dalam sampel ini.
Contoh 2: Anda melakukan pengukuran berulang terhadap berat badan seseorang selama 10 hari. Anda ingin mengetahui seberapa bervariasinya berat badan ini dari hari ke hari.
Dalam kedua contoh ini, Anda dapat menggunakan rumus standar deviasi di Excel dengan memasukkan data yang relevan ke dalam fungsi STDEV.S atau STDEV.P, tergantung pada apakah Anda memiliki data sampel atau populasi.
Menggunakan Fungsi STDEV.P dan STDEV.S
Perbedaan antara STDEV.P dan STDEV.S
Perbedaan utama antara fungsi STDEV.P dan STDEV.S adalah pada bagaimana mereka menghitung standar deviasi. STDEV.P digunakan untuk menghitung standar deviasi pada populasi, sementara STDEV.S digunakan untuk menghitung standar deviasi pada sampel. Dalam STDEV.P, pembaginya adalah jumlah populasi, sedangkan dalam STDEV.S, pembaginya adalah penjumlahan sampel dikurangi satu.
Kapan Menggunakan STDEV.P dan STDEV.S
Jika Anda memiliki data yang mewakili seluruh populasi, Anda harus menggunakan fungsi STDEV.P untuk menghitung standar deviasi. Namun, jika Anda hanya memiliki sampel dari populasi yang lebih besar, Anda harus menggunakan fungsi STDEV.S untuk mendapatkan perkiraan standar deviasi dari populasi tersebut.
Menafsirkan Hasil Standar Deviasi
Menafsirkan Hasil Standar Deviasi
Setelah Anda menghitung standar deviasi, penting untuk dapat menafsirkan hasilnya dengan benar. Standar deviasi yang tinggi menunjukkan bahwa data Anda memiliki variasi yang besar, sedangkan standar deviasi yang rendah menunjukkan variasi yang kecil. Jika standar deviasi sama dengan nol, ini berarti bahwa semua titik data memiliki nilai yang sama.
Perbandingan Standar Deviasi
Anda juga dapat membandingkan standar deviasi antara dua kelompok data atau variasi dalam waktu yang berbeda. Jika standar deviasi dari satu kelompok data lebih tinggi daripada yang lain, ini menunjukkan bahwa kelompok data tersebut memiliki variasi yang lebih besar.
Contoh: Anda memiliki dua kelompok data yang mewakili kinerja siswa dalam dua mata pelajaran yang berbeda. Jika standar deviasi nilai dalam satu mata pelajaran lebih tinggi daripada yang lain, ini menunjukkan bahwa nilai siswa dalam mata pelajaran tersebut lebih bervariasi dibandingkan dengan mata pelajaran lainnya.
Menggunakan Rumus Standar Deviasi dalam Analisis Data
Menggunakan Rumus Standar Deviasi dalam Analisis Data
Rumus standar deviasi di Excel dapat digunakan dalam berbagai analisis data, termasuk:
Distribusi Normal
Standar deviasi sering digunakan dalam analisis distribusi normal. Dalam distribusi normal, sebagian besar data berada di sekitar nilai rata-ratanya, dan standar deviasi digunakan untuk menentukan seberapa jauh data tersebar dari nilai rata-rata.
Uji Hipotesis
Standar deviasi juga digunakan dalam uji hipotesis. Uji hipotesis adalah prosedur statistik yang digunakan untuk membuat kesimpulan tentang populasi berdasarkan sampel data. Standar deviasi digunakan untuk menghitung tingkat signifikansi dan membandingkan hasil pengujian dengan ambang batas yang telah ditetapkan.
Contoh: Anda ingin menguji apakah rata-rata gaji di dua perusahaan berbeda secara signifikan. Anda dapat menggunakan rumus standar deviasi di Excel untuk menghitung standar deviasi gaji di masing-masing perusahaan, dan kemudian menggunakan uji hipotesis untuk membandingkan rata-rata gaji tersebut.
Menyajikan Standar Deviasi dalam Bentuk Grafik
Menyajikan Standar Deviasi dalam Bentuk Grafik
Visualisasi data dapat membantu kita memahami dan menganalisis data dengan lebih baik. Dalam menyajikan standar deviasi dalam bentuk grafik, Anda dapat menggunakan beberapa jenis grafik, termasuk:
Diagram Batang
Anda dapat menggunakan diagram batang untuk membandingkan stand
…ar deviasi antara beberapa kelompok data. Misalnya, Anda dapat membuat diagram batang untuk membandingkan standar deviasi ketinggian antara kelompok pria dan wanita.
Diagram Garis
Diagram garis dapat digunakan untuk menunjukkan perubahan standar deviasi dari waktu ke waktu. Misalnya, Anda dapat membuat diagram garis untuk menunjukkan perubahan standar deviasi suhu harian selama beberapa bulan.
Diagram Kotak Whisker
Diagram kotak whisker adalah grafik yang berguna untuk menunjukkan distribusi data dan rentang standar deviasi. Diagram ini dapat memberikan pemahaman yang lebih mendalam tentang variasi dalam data Anda.
Dengan menyajikan standar deviasi dalam bentuk grafik, Anda dapat dengan mudah membandingkan variasi antara kelompok data atau melihat perubahan variasi dari waktu ke waktu.
Menggunakan Rumus Standar Deviasi dengan Data yang Terbatas
Menggunakan Rumus Standar Deviasi dengan Data yang Terbatas
Ketika Anda hanya memiliki data yang terbatas, yaitu sampel dari populasi yang lebih besar, ada beberapa hal yang perlu diperhatikan dalam menghitung dan menginterpretasikan standar deviasi. Beberapa hal yang perlu dipertimbangkan adalah:
Ukuran Sampel
Ukuran sampel yang lebih kecil dapat menghasilkan perkiraan standar deviasi yang kurang akurat dibandingkan dengan populasi yang lebih besar. Semakin besar ukuran sampel, semakin akurat perkiraan standar deviasi.
Interval Kepercayaan
Ketika menggunakan sampel yang terbatas, penting untuk memperhatikan interval kepercayaan. Interval kepercayaan adalah rentang nilai yang mungkin mengandung nilai sebenarnya dari standar deviasi populasi. Semakin lebar interval kepercayaan, semakin tidak pasti perkiraan standar deviasi Anda.
Penggunaan Uji Hipotesis
Dalam penggunaan rumus standar deviasi dengan data yang terbatas, uji hipotesis juga dapat digunakan untuk menguji perbedaan signifikan antara kelompok data. Uji hipotesis dapat memberikan informasi lebih lanjut tentang apakah perbedaan yang diamati antara kelompok data adalah hasil kebetulan atau benar-benar signifikan.
Menangani Masalah Umum dalam Menggunakan Rumus Standar Deviasi di Excel
Menangani Masalah Umum dalam Menggunakan Rumus Standar Deviasi di Excel
Saat menggunakan rumus standar deviasi di Excel, ada beberapa masalah umum yang sering muncul. Berikut adalah beberapa masalah umum yang mungkin Anda temui dan solusinya:
Data yang Hilang atau Salah
Jika Anda memiliki data yang hilang atau salah, ini dapat mempengaruhi perhitungan standar deviasi. Pastikan data Anda lengkap dan benar sebelum menghitung standar deviasi.
Outlier atau Pencilan
Jika Anda memiliki outlier atau pencilan dalam data Anda, ini dapat mempengaruhi nilai standar deviasi. Pertimbangkan untuk menghapus atau menyesuaikan outlier sebelum menghitung standar deviasi.
Memahami Jenis Data
Pastikan Anda memahami jenis data yang Anda miliki dan memilih rumus standar deviasi yang tepat. Jika Anda memiliki data sampel, gunakan fungsi STDEV.S. Jika Anda memiliki data populasi, gunakan fungsi STDEV.P.
Terima kasih telah membaca artikel kami tentang rumus standar deviasi di Excel. Kami harap artikel ini memberikan pemahaman yang jelas dan komprehensif tentang penggunaan rumus ini. Dalam artikel ini, kami telah menjelaskan pengenalan standar deviasi, rumus standar deviasi di Excel, contoh penggunaannya, perbedaan antara STDEV.P dan STDEV.S, interpretasi hasil standar deviasi, penggunaan rumus standar deviasi dalam analisis data, penyajian standar deviasi dalam bentuk grafik, penggunaan rumus standar deviasi dengan data yang terbatas, serta cara menangani masalah umum yang mungkin muncul saat menggunakan rumus standar deviasi di Excel.
Jika Anda memiliki pertanyaan lebih lanjut, jangan ragu untuk meninggalkan komentar di bawah ini. Selamat menerapkan rumus standar deviasi di Excel!