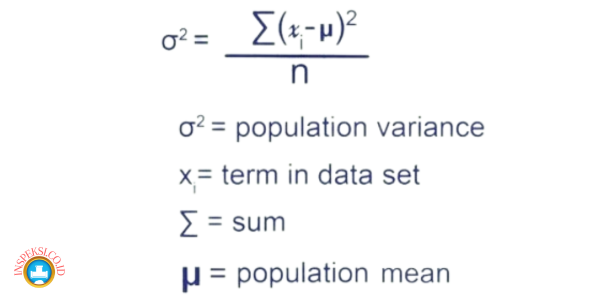Varian populasi adalah salah satu konsep penting dalam statistik yang digunakan untuk mengukur sejauh mana data tersebar dalam satu populasi. Dalam artikel ini, kita akan membahas secara rinci tentang rumus varian populasi, bagaimana menghitungnya, dan mengapa penting untuk memahami konsep ini dalam analisis data.
Pertama-tama, mari kita jelaskan apa itu varian. Varian adalah ukuran statistik yang menggambarkan seberapa jauh titik data individual tersebar di sekitar nilai rata-rata. Semakin besar varian, semakin bervariasi data kita. Dalam konteks varian populasi, kita tertarik untuk mengetahui sejauh mana data seluruh populasi tersebar, bukan hanya sampel yang diambil dari populasi.
Pengenalan Rumus Varian Populasi
Dalam sesi ini, kita akan memperkenalkan rumus varian populasi dan menjelaskan komponen-komponen yang terlibat dalam perhitungannya. Kita akan melihat bagaimana memahami rumus ini dapat membantu kita dalam menganalisis data statistik secara lebih mendalam.
Komponen-komponen Rumus Varian Populasi
Sebelum memahami rumus varian populasi, penting untuk memahami komponen-komponen yang terlibat dalam perhitungannya. Komponen utama dari rumus varian populasi adalah deviasi kuadrat dan jumlah anggota populasi. Deviasi kuadrat adalah selisih antara setiap titik data dan nilai rata-rata, yang kemudian dikuadratkan untuk menghilangkan nilai negatif. Jumlah anggota populasi adalah jumlah total titik data dalam populasi.
Rumus varian populasi dapat dinyatakan sebagai:
Varian = Σ (X – μ)² / N
Di mana:
- Σ (X – μ)² adalah jumlah dari deviasi kuadrat dari setiap titik data terhadap nilai rata-rata populasi.
- N adalah jumlah anggota populasi.
Manfaat Memahami Rumus Varian Populasi
Mengerti rumus varian populasi memiliki manfaat besar dalam analisis data statistik. Dengan memahami rumus ini, kita dapat:
- Mengukur sebaran data secara lebih akurat
- Melakukan perbandingan antara populasi yang berbeda
- Mengidentifikasi outlier atau data ekstrim
- Mengambil keputusan yang lebih baik berdasarkan karakteristik data
Memahami Konsep Deviasi dan Mean
Sebelum kita dapat menggunakan rumus varian populasi, penting untuk memahami konsep deviasi dan mean. Deviasi adalah ukuran statistik yang menggambarkan seberapa jauh titik data individual tersebar di sekitar nilai rata-rata. Mean atau rata-rata adalah jumlah dari semua titik data yang dibagi dengan jumlah total titik data.
Deviasi sebagai Ukuran Variabilitas Data
Deviasi merupakan ukuran statistik yang berguna dalam menentukan variabilitas data. Dalam konteks varian populasi, kita tertarik untuk mengetahui sejauh mana titik data individual tersebar di sekitar nilai rata-rata populasi. Semakin besar deviasi, semakin bervariasi data kita.
Mean sebagai Titik Pusat Data
Mean adalah titik pusat data yang merupakan jumlah dari semua titik data dibagi dengan jumlah total titik data. Mean memberikan gambaran tentang nilai tengah atau nilai yang paling umum dalam populasi. Dalam perhitungan varian populasi, kita akan menggunakan mean untuk menghitung deviasi setiap titik data terhadap nilai rata-rata.
Langkah-langkah Menghitung Varian Populasi
Dalam sesi ini, kita akan membahas langkah-langkah praktis untuk menghitung varian populasi. Kita akan melihat contoh perhitungan step by step dan memberikan penjelasan terperinci tentang setiap langkah yang terlibat dalam proses ini.
Langkah 1: Hitung Mean
Langkah pertama dalam menghitung varian populasi adalah dengan menghitung mean atau nilai rata-rata dari populasi. Untuk melakukan ini, jumlahkan semua titik data dan bagi hasilnya dengan jumlah anggota populasi.
Langkah 2: Hitung Deviasi Setiap Titik Data terhadap Mean
Langkah berikutnya adalah menghitung deviasi setiap titik data terhadap nilai rata-rata populasi. Untuk setiap titik data, kurangkan nilai rata-rata populasi dari titik data tersebut.
Langkah 3: Kuadratkan Setiap Deviasi
Setelah menghitung deviasi setiap titik data, langkah selanjutnya adalah mengkuadratkan setiap deviasi. Hal ini dilakukan untuk menghilangkan nilai negatif dan memastikan bahwa setiap deviasi memiliki kontribusi positif dalam perhitungan varian.
Langkah 4: Jumlahkan Semua Deviasi Kuadrat
Setelah mengkuadratkan setiap deviasi, jumlahkan semua deviasi kuadrat. Ini akan menghasilkan jumlah total deviasi kuadrat dari seluruh populasi.
Langkah 5: Bagi Jumlah Deviasi Kuadrat dengan Jumlah Anggota Populasi
Langkah terakhir adalah membagi jumlah deviasi kuadrat dengan jumlah anggota populasi. Ini akan memberi kita nilai varian populasi.
Contoh Penggunaan Rumus Varian Populasi
Bagaimana rumus varian populasi dapat diterapkan dalam kehidupan nyata? Dalam sesi ini, kita akan melihat beberapa contoh penggunaan rumus varian populasi dalam analisis data statistik. Kita akan melihat bagaimana varian populasi dapat memberikan wawasan yang berharga dalam memahami sebaran data.
Penggunaan Varian Populasi dalam Ekonomi
Dalam bidang ekonomi, rumus varian populasi dapat digunakan untuk mengukur risiko dan volatilitas dalam data keuangan. Misalnya, varian populasi dapat digunakan untuk mengukur seberapa bervariasinya tingkat pengembalian investasi dalam suatu portofolio saham. Semakin tinggi varian populasi, semakin besar risiko investasi tersebut.
Penggunaan Varian Populasi dalam Penelitian Sosial
Dalam penelitian sosial, varian populasi dapat digunakan untuk mengukur sebaran karakteristik sosial dalam sebuah populasi. Misalnya, varian populasi dapat digunakan untuk mengukur sebaran pendapatan rumah tangga dalam suatu negara. Dengan memahami seberapa bervariasinya pendapatan rumah tangga, pemerintah dapat merancang kebijakan yang lebih efektif dalam mengurangi kesenjangan ekonomi.
Perbedaan antara Varian Populasi dan Sampel
Ada perbedaan penting antara varian populasi dan varian sampel. Varian populasi mengukur variabilitas dalam seluruh populasi, sedangkan varian sampel mengukur variabilitas dalam sampel yang diambil dari populasi. Dalam sesi ini, kita akan menjelaskan apa perbedaan tersebut dan mengapa kita perlu memahami kedua konsep ini secara terpisah saat menganalisis data statistik.
Perbedaan dalam Rumus Perhitungan
Salah satu perbedaan utama antara varian populasi dan varian sampel adalah dalam rumus perhitungannya. Rumus varian populasi menggunakan jumlah anggota populasi sebagai pembagi dalam perhitungan, sedangkan rumus varian sampel menggunakan jumlah anggota sampel dikurangi satu sebagai pembagi.
Penggunaan Varian Populasi dan Sampel
Varian populasi dan varian sampel digunakan untuk tujuan yang berbeda dalam analisis data statistik. Varian populasi digunakan ketika kita memiliki data populasi lengkap, sedangkan varian sampel digunakan ketika kita hanya memiliki data sampel yang diambil dari populasi. Varian populasi memberikan estimasi variabilitas yang lebih akurat untuk seluruh populasi, sedangkan varian sampel memberikan estimasi variabilitas yang lebih konservatif karena menggunakan sampel yang lebih kecil.
Pentingnya Memahami Perbedaan ini
Memahami perbedaan antara varian populasi dan varian sampel sangat penting dalam analisis data statistik. Penggunaan yang tidak tepat dari rumus varian dapat menghasilkan estimasi yang tidak akurat dan kesimpulan yang salah. Oleh karena itu, penting untuk menentukan apakah kita memiliki data populasi lengkap atau hanya sampel, dan menggunakan rumus yang sesuai sesuai dengan kondisi tersebut.
Kelebihan dan Keterbatasan Rumus Varian Populasi
Seperti halnya konsep dan rumus matematika lainnya, rumus varian populasi memiliki kelebihan dan keterbatasan. Dalam sesi ini, kita akan membahas apa saja kelebihan dan keterbatasan dari rumus varian populasi dan bagaimana mengatasi keterbatasan tersebut.
Kelebihan Rumus Varian Populasi
Salah satu kelebihan utama rumus varian populasi adalah dapat memberikan estimasi yang akurat tentang sebaran data dalam seluruh populasi. Dengan menggunakan rumus varian populasi, kita dapat dengan lebih tepat mengukur variabilitas data dan memahami karakteristik populasi secara keseluruhan.
Keterbatasan Rumus Varian Populasi
Meskipun rumus varian populasi memiliki kelebihan, ada juga beberapa keterbatasan yang perlu diperhatikan. Salah satu keterbatasan utama adalah bahwa rumus varian populasi rentan terhadap data ekstrim atau outlier. Data ekstrim dapat memiliki pengaruh yang besar pada perhitungan varian populasi dan dapat menyebabkan estimasi yang tidak akurat.
Mengatasi Keterbatasan dengan Transformasi Data
Untuk mengatasi keterbatasan rumus varian populasi terhadap data ekstrim, kita dapat menggunakan metode transformasi data. Metode ini melibatkan mengubah data asli menjadi bentuk yang lebih terdistribusi normal atau menghilangkan outlier sebelum menghitung varian populasi. Dengan melakukan transformasi data, kita dapat mengurangi dampak data ekstrim pada perhitungan varian populasi.
Hubungan Varian dengan Standar Deviasi
Standar deviasi adalah ukuran statistik lain yang sering digunakan bersama dengan varian. Dalam sesi ini, kita akan menjelaskan hubungan antara varian dan standar deviasi, dan mengapa kedua konsep ini saling terkait erat dalam analisis data statistik.
Pengertian Standar Deviasi
Standar deviasi adalah ukuran statistik yang menggambarkan seberapa jauh titik data individual tersebar di sekitar nilai rata-rata. Dalam hal ini, standar deviasi memberikan informasi yang sama dengan varian, tetapi dalam satuan yang lebih mudah dipahami.
Hubungan antara Varian dan Standar Deviasi
Varian dan standar deviasi memiliki hubungan yang erat. Standar deviasi dapat ditemukan dengan mengambil akar kuadrat dari varian. Dalam rumus matematis, hubungan ini dinyatakan sebagai:
Standar Deviasi = √Varian
Mengapa Menggunakan Standar Deviasi
Standar deviasi sering digunakan dalam analisis data karena memberikan informasi yang lebih mudah dipahami daripada varian. Standar deviasi memberikan ukuran variabilitas dalam satuan yang sama dengan data asli, sehingga lebih intuitif untuk diinterpretasikan dan dibandingkan dengan nilai rata-rata atau titik data individual.
Menggunakan Rumus Varian Populasi dalam Analisis Regresi
Rumus varian populasi juga dapat digunakan dalam analisis regresi. Dalam sesi ini, kita akan melihat bagaimana rumus varian populasi dapat membantu kita dalam mengukur seberapa baik model regresi kita cocok dengan data yang ada.
Analisis Regresi dan Estimasi Variabilitas
Analisis regresi digunakan untuk menemukan hubungan antara variabel independen dan dependen dalam suatu model matematika. Dalam analisis regresi, kita tertarik untuk mengetahui sejauh mana variabilitas dalam data dapat dijelaskan oleh model regresi yang kita gunakan.
Menggunakan Rumus Varian Populasi untuk Mengukur Variabilitas Residual
Dalam analisis regresi, kita dapat menggunakan rumus varian populasi untuk mengukur variabilitas residual, yaitu perbedaan antara nilai yang diprediksi oleh model regresi dan nilai aktual dalam data. Dengan mengukur variabilitas residual, kita dapat mengevaluasi seberapa baik model regresi kita cocok dengan data yang ada.
Bagaimana Menginterpretasikan Nilai Varian Populasi
Hanya menghitung nilai varian populasi tidak cukup. Dalam sesi ini, kita akan membahas bagaimana menginterpretasikan nilai varian populasi dan apa arti nilai-nilai yang berbeda dapat memberikan dalam analisis data statistik.
Interpretasi Nilai Varian Populasi yang Rendah
Jika nilai varian populasi rendah, itu menunjukkan bahwa titik data individual cenderung mendekati nilai rata-rata populasi. Data lebih homogen dan tidak bervariasi secara signifikan. Ini dapat mengindikasikan bahwa ada konsistensi dalam data dan kurangnya outlier atau data ekstrim.
Interpretasi Nilai Varian Populasi yang Tinggi
Jika nilai varian populasi tinggi, itu menunjukkan bahwa titik data individual tersebar lebih jauh dari nilai rata-rata populasi. Data lebih heterogen dan bervariasi secara signifikan. Ini dapat mengindikasikan adanya variasi yang signifikan dalam populasi dan kemungkinan adanya outlier atau data ekstrim.
Perbandingan Variabilitas antara Populasi
Nilai varian populasi juga dapat digunakan untuk membandingkan variabilitas antara dua atau lebih populasi. Jika satu populasi memiliki varian populasi yang lebih tinggi daripada yang lain, itu menunjukkan bahwa populasi tersebut memiliki tingkat variabilitas yang lebih tinggi dan data yang lebih heterogen.
Kesimpulan
Dalam artikel ini, kita telah membahas secara detail tentang rumus varian populasi, bagaimana menghitungnya, dan pentingnya memahami konsep ini dalam analisis data statistik. Kita juga telah melihat contoh penggunaan rumus varian populasi dalam berbagai bidang dan hubungannya dengan konsep lain seperti standar deviasi dan analisis regresi. Dengan memahami rumus varian populasi dan bagaimana menggunakannya, kita dapat memperoleh wawasan yang lebih dalam tentang data statistik kita dan membuat keputusan yang lebih baik berdasarkan karakteristik data yang ada.